DM Suites guidé n°1

Soit \left(u_{n}\right) la suite définie par u_{0} = 5 et pour tout nombre entier naturel n, par : u_{n+1} = \dfrac{4u_{n} - 1}{u_{n} +2}

Si f est la fonction définie sur l’intervalle ]- 2~;~+ \infty[ par f(x) = \dfrac{4x - 1}{x + 2}, alors on a, pour tout nombre entier naturel n, u_{n+1} = f\left(u_{n}\right).

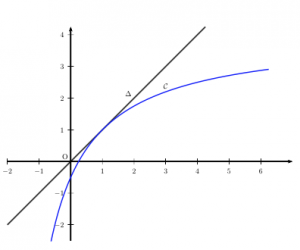
On donne  une partie de la courbe représentative \mathcal{C} de la fonction f ainsi que la droite \Delta d’équation y = x.cpirbe DM suites

  1. a. Sur l’axe des abscisses, placer u_{0} puis construire u_{1} u_{2} et u_{3} en laissant apparents les traits de construction.
    b. Quelles conjectures peut-on émettre sur le sens de variation et sur la convergence de la suite \left(u_{n}\right) ?
  2. a. Démontrer par récurrence que, pour tout nombre entier naturel n, on a u_{n} - 1 > 0.
    [peekaboo_link name= »aide2a »]Aide[/peekaboo_link]
    [peekaboo_content name= »aide2a »] Méthode 1 : Réduire u_{n+1}-1 au même dénominateur et utiliser  u_{n}-1>0 pour montrer que u_{n+1}-1>0
    Méthode 2 : Montrer par récurrence que u_{n} \geqslant 1 pour  tout n puis utiliser les variations de la fonction  f après avoir fait l’étude des variations de  f. [/peekaboo_content]
    [peekaboo_link name= »réponse2a »]Réponse partielle[/peekaboo_link]
    [peekaboo_content name= »réponse2a »] u_{n+1}-1=\dfrac{3(u_{n}-1)}{u_{n}+2} [/peekaboo_content]
    b. Dans cette question, toute trace de recherche, même incomplète, ou d’initiative même non fructueuse, sera prise en compte dans l’évaluation.
    Valider par une démonstration les conjectures émises à la question 1. b.
    [peekaboo_link name= »aide2b »]Aide pour variation de (u_{n})[/peekaboo_link]
    [peekaboo_content name= »aide2b »] Méthode 1 : Chercher le signe de  u_{n+1}-u_{n}
    Pour cela, réduire au même dénominateur
    Astuce : Reconnaître une identité remarquable (sinon chercher le signe d’un trinôme)
    Méthode 2 : Montrer par récurrence que u_{n+1} \geqslant u_{n} pour  tout n.
    On utilisera les variations de la fonction  f après avoir fait l’étude des variations de  f. [/peekaboo_content]
  3. [peekaboo_link name= »réponse2b »]Aide pour limite de u_{n}[/peekaboo_link]
    [peekaboo_content name= »réponse2b »]
    Partir de l’égalité u_{n+1} = \dfrac{4u_{n} - 1}{u_{n} +2} puis passer à la limite[/peekaboo_content]
  4. Dans cette question, on se propose d’étudier la suite \left(u_{n}\right) par une autre méthode, en déterminant une expression de u_{n} en fonction de n.
    Pour tout nombre entier naturel n, on pose v_{n} = \dfrac{1}{u_{n} - 1}.
    a. Démontrer que la suite \left(v_{n}\right) est une suite arithmétique de raison \dfrac{1}{3}.
    [peekaboo_link name= »aide1″]Aide 1[/peekaboo_link]
    [peekaboo_content name= »aide1″] Montrer que  v_{n+1}-v_{n}=\dfrac{1}{3} [/peekaboo_content]
    [peekaboo_link name= »réponse1″]Aide 2[/peekaboo_link]
    [peekaboo_content name= »réponse1″] A partir de l’énoncé,  exprimer v_{n+1} en fonction de  u_{n}.
    Réduire au même dénominateur v_{n+1}-v_{n}.
    Simplifier [/peekaboo_content]
    [peekaboo_link name= »réponse11″]Réponse partielle[/peekaboo_link]
    [peekaboo_content name= »réponse11″] On obtient  v_{n+1}=\dfrac{u_{n}+2}{3u_{n}-3} [/peekaboo_content]
    b. Pour tout nombre entier naturel n, exprimer v_{n} puis u_{n} en fonction de n.
    [peekaboo_link name= »aide2″]Aide 1[/peekaboo_link]
    [peekaboo_content name= »aide2″] (v_{n}) est arithmétique donc v_{n}=v_{0}+nr [/peekaboo_content]
    [peekaboo_link name= »réponse2″]Réponse[/peekaboo_link]
    [peekaboo_content name= »réponse2″] v_{n}=\dfrac{1}{4} + \dfrac{n}{3} [/peekaboo_content]
    [peekaboo_link name= »aide22″]Aide 2[/peekaboo_link]
    [peekaboo_content name= »aide22″] A partir de v_{n}=\dfrac{1}{u_{n}-1}  exprimer u_{n} en fonction de v_{n} [/peekaboo_content]
    [peekaboo_link name= »réponse22″]Réponse partielle[/peekaboo_link]
    [peekaboo_content name= »réponse22″] u_{n}=\dfrac{1}{v_n} +1    [/peekaboo_content]
    c. En déduire la limite de la suite \left(u_{n}\right).

 

Correction : Cliquer ici