Partie 1
On considère l’algorithme suivant :
Entrée :
un entier naturel.
Initialisation :
affecter à la valeur 1
affecter à la valeur 1
affecter à la valeur 0.
Traitement :
tant que
affecter à la valeur
affecter à la valeur
affecter à la valeur
.
fin du tant que
Sortie :
afficher
afficher .
Pour , quelles sont les valeurs de
et
affichées ?
Partie 2
Soit la suite définie par :
et, pour tout entier naturel
,
et la suite
définie sur N par :
.
- Pour un entier naturel
donné, que représentent les valeurs affichées par l’algorithme de la partie 1 ?
[peekaboo_link name= »aide1″] Vérification [/peekaboo_link][peekaboo_content name= »aide1″] Au 3ème passage de la boucle, on obtient u=11et S=21[/peekaboo_content] - Le but de cette question est d’exprimer
en fonction de
.
- Recopier et compléter le tableau suivant (pour
allant de 0 à 5) :
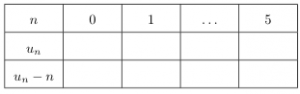 [peekaboo_link name= »aide2″]Vérification [/peekaboo_link][peekaboo_content name= »aide2″] pour n=3, on a u=11[/peekaboo_content]
[peekaboo_link name= »aide2″]Vérification [/peekaboo_link][peekaboo_content name= »aide2″] pour n=3, on a u=11[/peekaboo_content] - Quelle conjecture peut-on faire à partir des résultats de ce tableau ?
[peekaboo_link name= »aide3″]Aide [/peekaboo_link][peekaboo_content name= »aide3″] Les termes peuvent s’écrire comme une puissance d’un même nombre [/peekaboo_content] - Démontrer par récurrence que, pour tout entier naturel
.
- Recopier et compléter le tableau suivant (pour
- Le but de cette question est de calculer
en fonction de
et d’utiliser un résultat de la première partie pour contrôler l’exactitude de ce calcul.
- Exprimer en fonction de
les sommes :
et
[peekaboo_link name= »aide4″]Aide [/peekaboo_link][peekaboo_content name= »aide4″]est la somme des termes d’une suite arithmétique
etest la somme des termes d’une suite géométrique [/peekaboo_content]
- En déduire une expression de
en fonction de
.
[peekaboo_link name= »aide5″]Aide [/peekaboo_link][peekaboo_content name= »aide5″] Remplacer chaque terme de la somme par son expression puis faire des regroupements pour faire apparaître les sommes précédentes. [/peekaboo_content] - Vérifier le résultat obtenu dans la première partie pour
.
[peekaboo_link name= »aide6″]Aide [/peekaboo_link][peekaboo_content name= »aide6″] On doit trouvercomme dans la partie 1 [/peekaboo_content]
- Exprimer en fonction de
Correction : Cliquer ici
