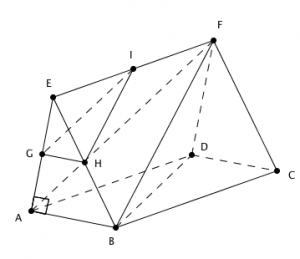
Répondre par VRAI ou Faux

1. Le point I appartient au plan (CBF)
   [peekaboo_link name= »question1″]Réponse[/peekaboo_link][peekaboo_content name= »question1″] VRAI.
   Le parallélogramme EFCB est contenu dans le plan (CBF) donc I appartient au plan (CBF)[/peekaboo_content]
2. Le point H appartient au plan (ADF)
   [peekaboo_link name= »question2″]Réponse[/peekaboo_link][peekaboo_content name= »question2″]FAUX.
   Le plan (ADF) contient le parallélogramme ADFE.
   H appartient à la droite (BE) qui n’appartient pas au plan (ADF) donc  H  n’appartient pas au plan (ADF)[/peekaboo_content]
3. Les points A, H et F sont alignés
   [peekaboo_link name= »question3b »]Réponse[/peekaboo_link][peekaboo_content name= »question3b »]FAUX.
   La droite (AF) est incluse dans le plan (ADF).
   H n’appartient pas au plan (ADF)  donc H n’appartient pas à la droite (AF) et donc H, A et F ne sont pas alignés[/peekaboo_content]
4. Les droites (IH) et (CF) sont sécantes.
   [peekaboo_link name= »question4″]Réponse [/peekaboo_link][peekaboo_content name= »question4″]VRAI.
   Rappel : Dans l’espace, deux droites sont sécantes si elles sont coplanaires et non parallèles.
   (IH) et (CF) sont coplanaires car contenues dans  le plan (CBF), plan contenant le parallélogramme EFCB.
   (IH) et (CF) n’étant pas parallèles, elles sont donc sécantes[/peekaboo_content]
5. Les droites (BF) et (CD) se coupent
   [peekaboo_link name= »question4b »]Réponse[/peekaboo_link][peekaboo_content name= »question4b »]FAUX.
   D n’appartient pas au plan (BCF) donc (BF) et (CD) ne sont pas coplanaires, elles ne peuvent donc pas être sécantes.[/peekaboo_content]
6. Les droites (IH) et (BF) sont parallèles
   [peekaboo_link name= »question5″]Réponse [/peekaboo_link][peekaboo_content name= »question5″]VRAI.
   Rappel : théorème des milieux dans un triangle :
   Dans un triangle, si une droite passe par les milieux de deux côtés  alors elle est parallèle au troisième côté.
   Dans le triangle EFB, I est milieu de [EF] et H est milieu de [EB] donc (IH) est parallèle à (BF)[/peekaboo_content]
7. Les droites (AF) et (BD) sont parallèles.
   [peekaboo_link name= »question6″]Réponse[/peekaboo_link][peekaboo_content name= »question6″]FAUX.
   B n’appartient pas au plan (ADF) donc les points A, F, B et D ne sont pas coplanaires. Les droites (AF) et (BD) ne sont pas coplanaires et  donc ne peuvent pas être parallèles[/peekaboo_content]
8. Les plans (GHI) et (ABF) se coupent
   [peekaboo_link name= »question8″]Réponse[/peekaboo_link][peekaboo_content name= »question8″] FAUX.
   D’après le théorème des milieux dans un triangle , on a (GH) parallèle à (AB) et (HI) parallèle à (BF) donc le plan (GHI) contient deux droites parallèles à deux droites du plan (ABF).
   Les deux plans sont donc parallèles et même strictement parallèles
   [/peekaboo_content]
9. La droite (DC) ne coupe pas le plan (GHI)
   [peekaboo_link name= »question9″]Réponse[/peekaboo_link][peekaboo_content name= »question9″]VRAI.
   (DC) est parallèle à (AB) car ABCD parallélogramme.
   (AB) est parallèle à (GH) d’après le théorème des milieux dans un triangle.
   On a donc (DC) parallèle à (GH) et donc (DC) parallèle au plan (GHI).
   On a (DC) strictement parallèle au plan (GHI) et donc (DC) ne coupe pas le plan  (GHI)[/peekaboo_content]
10. Le triangle ABF est isocèle
    [peekaboo_link name= »question10″]Réponse[/peekaboo_link][peekaboo_content name= »question10″]FAUX.
    Les parallélogrammes AEFD et EFCB ont le côté [EF] en commun.
    La longueur EB est plus grande que la longueur AE car [EB] est l’hypoténuse du triangle rectangle AEB.
    On en déduit que la longueur de la diagonale [BF]  du parallélogramme (BCFE) est plus grande que la longueur de la diagonale [AF] du parallélogramme AEFD et donc BF différent de AF et le triangle ABF n’est pas isocèle en F [/peekaboo_content]